一級建築士試験構造力学のポイントは？12の計算問題対策とは

一級建築士の学科試験には構造という科目があり、前半に7つの計算問題が出ますよね。

今回は一級建築士試験構造力学の計算問題を解くための12のポイントについて見ていきましょう。

この12のポイントを抑えれば、力学の問題の8割を解けるようになると言われています。

実際に、問題をやり込む前にポイントを押さえたほうが合格に近づきますから、まずはこのページでポイントを抑えましょう。

問題はそれからです。

静定梁・静定ラーメン

静定梁、静定ラーメンの問題は横着せずに、かならず反力を求めてから応力を求めます。

1. 支点反力を仮定して、つりあい条件式（ΣX=0、ΣY=0、ΣM＝0M=0）を立てて、支点反力を求める。
2. ある点の応力を求める場合、その点で架構を切断し、どちらか一方の外力及び支点反力による応力の和を求める。

なぜだか解けないな、と思ったら、もう一度基本に立ち返って、反力をしっかり出しているか？を確認しましょう。

静定トラスの軸方向力

トラスを苦手としている方が多いですが、しっかり基本を守れば簡単ですよ。

1. 支点反力を求める。
2. 求める材を含んでトラスを切断し、それぞれの材の軸方向力を仮定する。
3. 力のつりあい条件式を用いて解を求める。
   ΣM=0を用いる場合は、求める材以外の仮定した軸方向力の作用線の交点を中心とした式とする。
   斜材はΣY=0を用いることで、効率よく解を得られるケースがある。

トラスも焦って解くのではなく、まずは落ち着いて反力を求めることを忘れないようにしましょう。

断面二次モーメント、断面係数

断面の性質は公式を覚えることが先決です。

1. 図心軸についての長方形の断面二次モーメントは、I=bh³/12を用いて求める。
2. ロの字型やH形の断面二次モーメントは、長方形の断面二次モーメントの和・差を用いて求める。
3. 断面係数Zは、断面形状に関係なく、断面2次モーメントを図心軸から縁までの距離で除して求めることができる。

断面係数ZはZ=bh²/6を用いて求めます。

応力度

応力度はちょっと難しいですが、立体を意識して考えるとイメージ湧くと思います。

1. その断面の図心に生じる軸方向力N、曲げモーメントMを求める。
2. σ＝-N/A±M/Z(=-N/A±Mx/Zx±My/Zy)の式に代入し、引張応力度・圧縮応力度を求める。

梁のたわみ、たわみ角

たわみの公式は必ず全部覚えましょう。

語呂合わせで覚えると楽ですよ。

1. 代表的なたわみ、たわみ角の式を公式として記憶し、条件をあてはめて解を求める。
2. 単純に公式があてはまらない場合は、公式を組み合わせて解を求める。
3. モールの定理を用いる。

モールの定理でなければ解けない問題はほとんど出ません。

理解しなくても良いです。その分違う分野の何かを覚えるのに時間を費やすのも効率的です。

座屈荷重の大小関係

座屈荷重の問題は柱だったりラーメンだったり片持ち柱だったりしますが、基本は同じです。

1. 支持条件により座屈長さlkを求める。
2. EI/h²の大小関係より、座屈荷重Pkの大小関係を求める。

ラーメンに生じる応力

ラーメンは柱と梁からなる構造ですが、基本的には材の両端に生じるモーメントの和をスパン寸法で割ることで求めることができます。

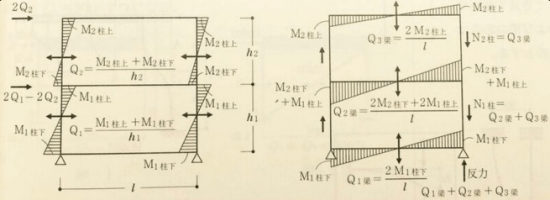
柱のせん断力の分担割合

柱のせん断力の分担割合はたわみの公式の組み合わせです。

1. それぞれの柱が負担するせん断力をQA、QBと仮定する。
2. それぞれの柱の水平変位をδA、δBとし、QA、QBの式で表す。

   柱Aが両端固定の場合　Qh3/12EI＝QAｈ・A³/12EA・IA＝δA
   柱Bが一旦固定他端ピンの場合　Qh³/3EI＝QB・ｈB³/3EB/IB＝δB

3. QA、QBをδA、δBの式で表す。
   QA＝12EA・IA・δA/hA³　QB＝3EB・IB・δB/hB³
4. 共通項を整理し、比を求める。
   QA:QB＝12EA・IA/hA³（δA）：3EB・IB/hB³（δB）＝12EA・IA/hA³：3EB・IB/hB³
   梁が剛体なのでδA＝δB。

ちょっと時間かけて理解しましょう。

ラーメンの水平変位と水平剛性

ラーメンの水平変位と水平剛性です。

3階建ての建物の各層の層間変位は次式で求められます。
δ1＝P1+P2+P3/K1
δ2＝P2+P3/K2
δ3＝P3/K3
頂部の水平変位δは各層の層間変位の和（δ1+δ2+δ3）となります。

それぞれの問題で求められる変位が異なるので、問題文をよく読みましょう。

固有周期の大小関係

固有周期です。

地震との関連がありますから、必ず出題されると考えて確実に押さえておきましょう。

固有周期Τの大小関係は、すべての振動モデルが同条件（1質点系またはラーメン）であれば√(m/k)または√（ml³/EI）の大小関係で求めることができる。

全塑性モーメント

全塑性モーメントについてです。

1. 軸方向ロy句が作用していない場合、引張側の合力Τまたは圧縮側の合力Cに応力中心間距離jを乗じて求める。
   （Mp=C×j＝Τ×j）
2. 軸方向力が作用している場合、軸方向力に抵抗する部分と曲げモーメントに抵抗する部分に分解し、曲げモーメントに抵抗する部分のMp＝Τ×j＝C×jで求める。

崩壊荷重

ラストです。

崩壊荷重についてです。

1. 崩壊機構が与えられている場合
   塑性ヒンジの回転角θ及び崩壊荷重Puの変位δを求め、ΣPu・δ＝ΣMp・θの関係式よりPuを求める。
2. 崩壊機構が与えられていない場合
   想定される崩壊機構のそれぞれのPuを上の手順で求め、最も小さい値が崩壊荷重となる。

ヨシヒロ

以上、今回は一級建築士試験構造力学のポイント12を紹介しました。

それぞれ参考書や問題集の解説をよく読んで理解しましょう。

時間がかかりますが、どうしても理解できない部分はとりあえず後回しして、理解しやすいところからやっていきましょう。

限られた時間の中で、効率よく学習していきましょう。